| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 스플라인
- PRML
- 혼자공부하는SQL
- 제주도여행
- 티스토리챌린지
- 클러스터형인덱스
- 보조인덱스
- GenAI
- Github
- 책리뷰
- RStudio
- R
- 김호연작가
- 디지털마케팅
- PRIMARY KEY
- 영국여행
- 유럽여행
- digital marketing
- 에이바우트
- 스토어드 프로시저
- Linux
- SQL
- Jupyter notebook
- 오블완
- 런던
- 맛집
- 독후감
- 제주도
- 혼공S
- 제주2주살이
- Today
- Total
Soy Library
[PRML] Ch1-(1). 예시:다항식 곡선 피팅 본문
이 예시는 회귀 문제를 다룬다. 여기서는 $sin(2\pi x)$에 약간의 noise를 추가해 데이터를 생성하였다.
$$ \mathbf{t} = sin(2\pi \mathbf{x}) + \varepsilon $$ 이때 $\mathbf{t} = (t_1, t_2, ...., t_N)^T$, $\mathbf{x} = (x_1, x_2, ..., x_N)^T$이다. 오차는 가우시안 분포를 따른다. 즉, N개의 input vector $\mathbf{x}$에 대해서 N개의 output vector $\mathbf{t}$가 있는 것이다.

이제 우리는 이 데이터를 이용해서 곡선을 fitting 시키고, 이 함수를 통해 어떠한 input $\hat{x}$이 주어졌을 때 타켓 변수 $\hat{t}$를 예측한다.
해당 곡선을 fitting하는데 있어서 다음과 같이 다항식을 먼저 생각해볼 수 있다.
$$ y(x, \mathbf{w}) = w_0 + w_1x + w_2x^2 + w_3x^3 + ... + w_Mx^M = \sum_{j=0}^Mw_jx^j$$
여기서 $M$은 이 다항식의 차수(order)이다. 위의 함수는 $x$에 대해서는 비선형이지만 $\mathbf{w}$에 대해서는 선형이다. 이 다항식은 train data를 통해 fitting을 시키는데 이때 우리는 오차함수(error function)의 개념을 사용한다.
오차함수(Error function)란, train data의 원래의 표적 데이터 $\mathbf{t}$와 우리가 fitting한 함수값 $y(x, \mathbf{w})$간의 오차를 측정하는 것으로 다음과 같이 이 오차를 제곱하여 합산할 수도 있다.
$$E(\mathbf{w}) = {1 \over 2} \sum_{n=1}^N[y(x_n, \mathbf{w}) - t_n]^2$$ 위의 오차함수를 $\mathbf{w}$에 대해 미분하면, 이를 최소화하는 $\mathbf{w^*}$를 찾음으로써 곡선 fitting 문제가 해결된다.
이제 모델비교 또는 모델 결정의 단계이다. 즉, 차수 M을 결정해야 하는 것이다. 만약 이 차수가 너무 크면 overfitting의 문제가 있고 반대로 너무 작으면 underfitting의 문제가 생긴다. 새로운 데이터 100개를 생성하여, 추정된 $\mathbf{w^*}$를 이용하여 M값에 따라 일반화의 성능이 어떻게 변화는지 살펴볼 수 있다. 이는 잔차로 비교할 수도 있고, 여기서는 평균 제곱근 오차(root mean square error, RMS error)를 사용하여 비교해보도록 하겠다. 평균 제곱급 오차의 식은 다음과 같다. $$E_{RMS} = \sqrt{2E(\mathbf{w^*}) / N}$$ 여기서 N으로 나눔으로써 데이터 사이즈가 다른 경우에도 비교할 수 있고(100개의 test data를 뽑았을 때랑, 10개의 test data를 뽑았을 때를 말하는 건가), 제곱근을 취함으로써 $E_{RMS}$가 표적값 $t$와 같은 크기를 가지도록 한다.

위 그래프는 각각의 차수 $M = 0, 1, ..., 9$에 대해서 평균제곱오차 그래프를 비교한 것이다. train데이터에서의 오차는 당연히 M=9일 때가 0이 될 것이다. 이는 모든 표적값을 지나게끔 모델을 fitting시켰기 때문이다.(해당 다항식은 $w_0, w_1, ..., w_9$의 열 개의 계수를 통해 10차의 자유도를 가지며, 우리가 피팅에 사용한 데이터 포인트의 숫자도 10개이기 때문이다.) 하지만 test데이터에서의 오차가 제일 크게 나온다. overfitting을 시켰기 때문에 그래프가 심하게 진동하고 이는 원데이터를 잘 예측하지 못한다는 결과를 초래한다.
모델의 복잡도를 일정하게 유지시킬 때는 사용하는 데이터 집합의 수가 늘어날수록 과적합 문제가 완화되는 것을 확인할 수 있다. 하지만 비교적 복잡하고 유연한 모델을 제한적인 숫자의 데이터 집합을 활용하여 피팅하려면 어떻게 해야할까? 그 기법 중에 하나는 정규화(regularization)이다. 이는 다음과 같이 오차 함수에 계수가 커지는 것을 막기 위한 penalty term을 추가하는 것이다. $$ \tilde{E}(\mathbf{w}) = {1 \over 2}\sum_{n=1}^N[y(x_n, \mathbf{w}) - t_n]^2 + {\lambda \over 2} ||\mathbf{w}||^2$$ 여기서 $||\mathbf{w}|| \equiv \mathbf{w^T}\mathbf{w}$이고 $\lambda$는 penalty term의 상대적인 중요도를 결정한다.
위의 식 또한 closed form이기 때문에 minimizer를 찾는 것은 미분을 통해 가능하다. 이 방법을 shrinkage method라고 하고 ridge regression(릿지 회귀)이라고 부른다. Neural Network 맥락에서는 이를 weight decay(가중치 감쇠)라 한다.

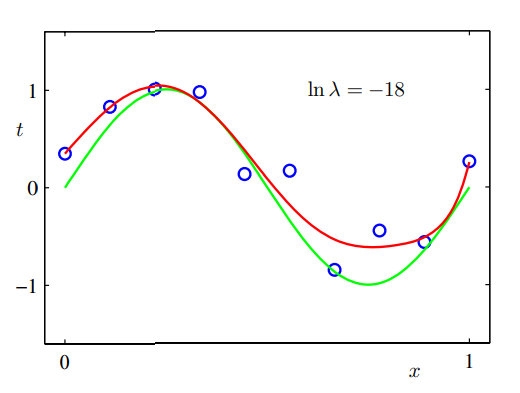
$\lambda$ 값이 커질수록 curve는 0으로 shrink된다.
지금까지의 결과를 바탕으로 모델 복잡도를 잘 선택하는 단순한 방법 하나를 생각해보면, 그것은 데이터 집합을 훈련 집합(training set)과 검증 집합(validation set, hold-out et)으로 나누는 방법이 있다. train set에서는 계수 $\mathbf[w]$를 결정하는 데 활용하고 검증 집합은 모델 복잡도($M$이나 $\lambda$)를 최적화하는데 활용할 수 있다.
Reference
Pattern recognition and Machine Learning, Christopher M. Bishop.
패턴인식과 머신 러닝, 크리스토퍼 비숍, 김형진 옮김.
'Study > PRLM' 카테고리의 다른 글
| [PRML] Ch1-(0). 소개 (0) | 2020.09.13 |
|---|
